|
Home ||
High Power Rocketry ||
Experimental Rocketry
Ignition & Igniters
Ignition Time, What's
the Difference?
So you have gone through the design process, designed a 4 grain 1" motor,
built your rocket, your launch pad, your launch system, it is time to put
the igniter in the motor and launch this puppy! It doesn't matter what
igniter, or how it is put in the motor as long as it ignites the grains and
fires the motor. Right? Yes, that is right if you don't care how
high the rocket goes or how efficient your motor is. Otherwise, you
wrong. Your engines performance IS affected by its
ignition and that is dependant on the igniter and how it is loaded into the
motor.
When I first started testing motors, I was anxious to burn some and I hadn't
put any time into figuring out how to make igniters. I had some fuse
left over from my pyrotechnic days a few decades ago and I figured that was
good enough. I had a limited supply so I cut short lengths and put
them just inside the nozzle. Fortunately, potassium nitrate and sugar
fuel ignites easily so the fuse lit the motors successfully. They
would fizzle, smoke, and sit there for a few seconds as the smoke poured out
more and more and finally a crescendo as the motor came up to full pressure
and then in a split second, the motor was done firing. Even though I
had not taken the time to make igniters, I had built an impulse recording
setup since that was the whole reason for building the motors, to see what
the thrust curve looked like and what specific impulse I could achieve.
The results were dismal and I wasn't sure why. I little more reading
revealed what should have occurred to me as an engineer anyway if I had just
thought about it for a minute or two.
Lets take a hypothetical motor and look at the difference between a
theoretical instantaneous ignition to full power and one that just takes
three seconds to come up to full pressure. Here is our hypothetical
motor:
GRAINS
Potassium Nitrate, Sucrose propellant
.996" O.D. (for a 1" PVC pipe case)
.375" Core (I.D.)
1.75" length
4 grains
Nozzle throat dia: 23/64" (just 1/64" smaller than the core).
Plugging that into FPRED, V3.3, we get the following:
|
|
 |
Maximum Pressure: 308 psi
Maximmum Thrust: 38 psi
Impulse: 137 N-Sec
Thurst Duration: 0.77 seconds
Time at Maximum Thrust: 0.42 seconds.
Specific Impulse: 98.96 seconds |
Now lets assume we have a slow start.
It doesn't just take time to build up pressure, it is burning the propellant
at a low pressure and with no thrust to start with. The propellant is
wasted and the longer it burns at a low pressure, the larger percentage of
the propellant is used up and the lower the total impulse, the lower the
specific impulse (lower effeciency) and the less altitude the rocket will
achieve.
Lets assume it takes three seconds to
build up to full pressure. The simulation doesn't capture what
actually happens very well because it assumes it is a steady ramp up and
actually it is more like an exponential rise but lets first look at the
simulation and see what it looks like.
|
|
 |
Maximum Pressure: 114 psi
Maximmum Thrust: 12.9 psi
Impulse: 42.8 N-Sec
Thurst Duration: 1.69 seconds
Specific Impulse: 30.88 seconds |
First note that the scales on the two
graphs are different and if they were superimposed they would look like
this:
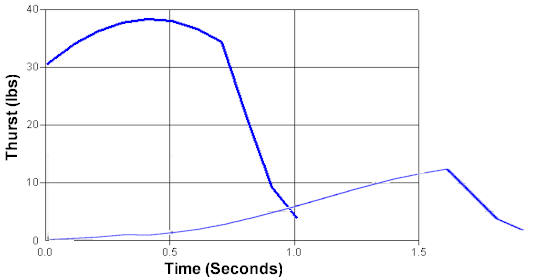
The simulation doesn't even start until
it starts building thrust. Before that, it is just burning off
propellant with nothing happening. The total area under the curves is
the total impulse so you can see that there is significantly less when it
takes time to build up to pressure. By the time it does start building
up pressure, there isn't enough propellant left to build up to operating
pressure.
What is happening is that the
propellant starts burning near the nozzle and there isn't enough surface
area burning at first to build up pressure. The flame resists moving
up the core because what is burning pushes the gases in the opposite
direction towards the nozzle. So it burns progressively up away from
the nozzle slowly as the propellant is burned up. The first grain is
probably entirely consumed before the flame reaches the last grain.
My tests using a fuse was with 1/2" pvc
pipe motors and with a fuse not in very far, the burn time was about twice
as long and the total impulse about 60% of what it was using an electric
igniter.
When you put an electric igniter at the
opposite end from the nozzle, the hot gases from the burning at the opposite
end will flow down through the entire core and out the nozzle. This
will ignite the rest of the core very quickly.
With sugar propellant, this happens
very quickly because the propellant ignites easily. Composite and
epoxy propellants ignite more slowly so the ignition process should be
optimized as much as possible.
The size of the igniter can be used for
this fine tune procedure. The igniter can be designed to burn very
fast and so produce hot gases that will actually pressurize the motor while
it is igniting the rest of the propellant burning surface. It can be
calculated so that it produces just enough gas to fully pressurize the core.
If it produced too much gas, it can over-pressurize the motor and cause it
to burst.
For Sugar motors, any fast burning
igniter with a significant amount of pyrogen will work and we won't try to
do that optimization.
Anatomy of an Igniter
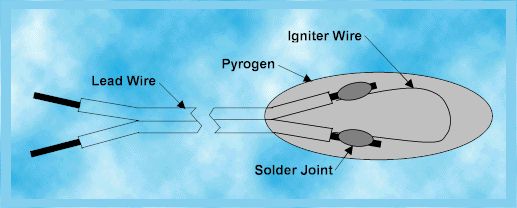
| |
|
Side Note on definitions. Pyrogen:
1) any substance characterized by its great flammablility,
2) any substance that can cause a rise in body temperature.
Used to coat electric matches. Pyrolant: Metal-based
pyrotechnic compositions generally characterized by high combustion
temperatures (< 2000 K) and high amounts of condensed reaction
products. Typical use is as pyrotechnic initiators.
Pyrotechnic initiator: (also initiator or
igniter) is a device containing a pyrotechnic composition used
primarily to ignite other, more difficult to ignite materials, e.g.
thermites, gas generators, and solid-fuel rockets. The name is often
used also for the compositions themselves |
|
|
An igniter, as shown in the diagram
above, normally is just a long two conductor lead wire with an igniter wire,
also called a bridge wire, attached across the two lead wires at one end.
That end is then dipped in a pyrogen which is a chemical mixture that will
catch fire easily and burn hot to ignite the rocket motor propellant.
The actual configuration of igniters varies greatly but except for some
small model rocket igniters, all have these three components. Because
a model rocket motor is small, the igniter wire does not need to be attached
to a lead wire. The launch system alligator clips are attached
directly to the igniter wire and the pyrogen only covers a portion of the
igniter wire. The lead wire is long enough so that the pyrogen end can
be pushed all the way through the motor core to the forward end of the
rocket and the other end can protrude out the nozzle where the launch system
alligator clips can be attached.
How an Igniter Works
An igniter works very similar to a
standard incandescent light bulb. The igniter wire serves the same
function as the filament in the light bulb. When a voltage is applied to a
light bulb, a current flows through the filament and the filament heats up.
It becomes so hot that it passes the red hot stage and into the white hot
range and so emits white light which is the intent of a bulb. An
igniter uses the other part of the phenomenon, the heat. The heat from
the hot igniter wire ignites the pyrogen which burns and throws off burning
bits of the pyrogen in all directions which most land on the rocket motor
fuel and so ignite it and starts the motor operating. A light bulb
filament is made from tungsten and the bulb itself has a vacuum. This
combination allows the light bulb to continue to light for many hours
(usually many less than what the package claims). Since an igniter is
a one use device, it only needs to stay hot long enough to ignite the
pyrogen and that is only a split second. The igniter wire experiences what
Edison experienced in his hundreds of failed attempts -- the extreme heat
melts or vaporizes the igniter wire in one place or in its entirety.
When this happens, current obviously quits flowing and no more heat is
generated. We only need a moment of that extreme heat to ignite the
pyrogen so in our case, that is acceptable.
The igniter wire can be made from any
number of materials but the most common is nichrome. Nichrome is an
alloy of nickel and chromium and has a higher resistance than other common
wire used just to carry current such as aluminum or copper. It also
has a higher resistance than iron, steel, or stainless steel.
Several factors affect the operation
and so construction of an igniter: wire material, wire
diameter, wire length, voltage, and heat dissipation capability. The
heat dissipation capability has the least affect. In a light bulb,
there is a near vacuum which is an almost perfect insulator of heat by
conduction. There are three methods of heat conduction: conduction,
convection and radiation. The light bulb gets hot to the touch purely
from radiation from the white hot filament.
Since the igniter wire is dipped in a
pyrogen which is in immediate contact with the igniter wire, the heat
transfer is mostly from conduction and some radiation but there is almost no
dissipation. All of the heat from the igniter is transferred to the
pyrogen. If there is enough heat, the pyrogen will ignite and burn.
The lead wires need to carry the
current used by the igniter without getting hot while the igniter wire needs
to get very hot. To do this, we need the lead wires to have low
resistance which means the conductor will probably be copper and the gauge
should be 24ga to 16ga (the smaller the number, the larger the wire) but
will depend on the design. On the other hand, the igniter wire needs
to be very small and have a higher resistivity than the lead wire.
Actually, there is a tradeoff between the diameter of the wire and
resistivity since a smaller diameter wire could have the same total
resistance as a larger diameter wire with more resistivity except the larger
diameter wire will require more watts or BTUs to get to the same temperature
in the same time due to the larger volume and mass. Usually,
the igniter wire will be between 34ga and 40 ga.
Igniter Calculations
Current and Power
Here we need to get more specific than
just saying heat. We normally think of heat as just temperature but
heat is temperature and power which can be expressed in different units such
as watts or BTU's. We then add one more monkey wrench into the
equation, time, which then determines energy. Power applied over time
equals energy. We need a certain amount of energy to make an igniter
work but that energy must also generate a high enough temperature. We
could use up a whole lot of energy an never ignite the pyrogen if that
energy didn't produce a high temperature. Lets look at some important
equations here.
|
I = current in amps (A)
E = voltage in volts (V)
R = resistance in ohms (Ω).
P = power in watts (W)
L = length in inches (in)
A = area in square inches (in2
)
V = volume in cubic inches (in3)
ρ
= resistivity in ohm inches
cir mil = π/4,000,000 in2
π =
3.1415927
r = radius
d = diameter
|
I = E/R, R = E/I and E = IR (Ohms Law)
P = I2R, P = E2/R
and P = EI
A =
πr2
= πd2/4
R = ρL/A =
4ρL/πd2
|
To measure the resistance, R, one can apply a known voltage across the
resistance, measure the current flow, I, and use Ohm's Law to get R from V=RI.
When you use a multimeter, that is what is happening inside and the results
are shown directly on the display.
We need to first find out what the
current will be in the igniter, the watts of power generated and then decide
if that will heat the igniter white hot for long enough and over enough area
to ignite the pyrogen. A lot more heat will be generated over a coiled
igniter wire using an inch or so of wire to be heated than an igniter wire
wrapped over the edge of a chip of circuit board. One being sold uses
a 50 gage nichrome wire which itself will generate a lot less heat per inch
than a 36 or 40 gage nichrome wire and then instead of using a coil, you
only have about the amount of the thickness of the board, proably about
1/16" (.0625"). This will take a very low current to heat the wire
white hot but the total power will be a small fraction of that generated by
a more robust igniter. As long as the pyrogen is ignited, the advantage is that very small batteries can be used to save weight,
especially on smaller models or the same 9V battery can be used for
multiple launches.
Battery draw down
Batteries have internal resistance and
so when they are connected to low resistance across the battery terminals,
the battery voltage will drop until ohms law is satisfied. Ohms law is
E = IR where E is voltage in volts, I is current in amps, R is resistance in
ohms. If a battery is rated at 9 volts, and a low resistance, say 0.1
ohm is placed across the terminals, the current that would theoretically
flow would be 9/.1 = 90 amps. If the battery had an internal
resistance of 4.5 ohms then it could only deliver 9/4.5 = 2 amps, not 90.
So the near short circuit the .1 ohm resistance load supplies to the battery
forces the battery to drop most of the voltage across the internal
resistance so there is little voltage left across the .1 ohm load. The
circuit would actually look like this:
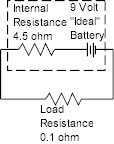
The actual resistance would then be 4.6
ohm. 0.1/4.6 = .0127 is the portion of the 9V the load would see so 9V
* 0.0127 = 0.145V. The low resistance would drop the voltage at the
terminals of the battery from 9V down to 0.145V and the current would be
almost the max that could be delivered or 2 amps.
I have seen many explanations on the
web talking about the amp-hours (or milliamp-hours) of a battery and how a
10 amp-hour battery can deliver .1 amps for 20 hours or 1 amp for 10 hours
and so on. This is not true because the higher the drain on the
battery, i.e. the higher the current pulled from the battery, the lower the
amp-hour capacity is going to be. It is not linear. You can get
the rated amp-hours out under low loads but not at high loads such as firing
igniters. Also, as the battery looses its life, the internal
resistance goes up and it will not be able to deliver the same current as
when it is new. This is one reason that when you fly a rocket with a
9V battery that runs the altimeter, it not only runs the electronics of the
altimeter but also fires both igniters if both are used. It is common
to either have an igniter fire at apogee and at a lower altitude or both
fire, one a couple seconds after the other, both at apogee. There is
no reason to take the chance that the battery could not do it again.
It is often a matter of an expensive rocket worth a hundred or hundreds of
dollars and a two dollar battery. If the battery fails, you have lost
your entire rocket.
Alkaline batteries have a relative high
internal impedance while NiCad batteries have low internal resistance and so
can deliver a much higher current. There are other batteries which
also have low internal resistances. Which battery is chosen depends on
what the current requirement of the igniter is.
I have not yet found a chart of battery
internal resistances or maximum (short circuit) current capabilities.
It would certainly be nice to be able to list that here.
Temperature
What is the temperature the igniter
will achieve? It depends purely on the melting temperature of the wire
used. See the Misc.
Tables page, Properties of Metals. As long as there is enough
current, the igniter wire will heat up until it reaches the melting
temperature of the wire at which point it will melt apart and open the
circuit. By this time, it should have ignited the pyrogen around it.
The temperature should be considerably higher than the ignition temperature
of the pyrogen to insure ignition. It actually would be possible for
the temperature to be insufficient if the worst combinations were used.
For example, Aluminum melts at 1220 °F
and if potassium perchlorate and sucrose were the pyrogen, ignition
temperature 1098 °F, the temperatures
would be too close together. Obviously, you would never use aluminum
wire for a bridge wire anyway. For any pyrogen, there is a
specific temperature at which it will ignite but this depends on the
proportions of the ingredients, the particle size of each ingredient, and a
host of other things. For example,
| |
| Black powder: |
|
| Potassium nitrate 80%,
charcoal 10%, sulfur 10% |
572 °F
(300 °C) |
| Potassium nitrate 80%,
charcoal 20%, sulfur 0% |
824 °F
(440 °C) |
| Potassium chlorate - charcoal (stoichiometric
ratio) |
635 °F
(335 °C) |
| Potassium percholorate - charcoal (stoichiometric
ratio) |
860 °F
(460 °C) |
| Potassium chlorate - sucrose |
882 °F
(472 °C) |
| Potassium perchlorate - sucrose |
1098 °F
(592 °C) |
|
|
|
Note: potassium chlorate is
sensitive and can be dangerous. Its use is highly discouraged.
Substituting potassium chlorate for potassium nitrate, i.e. mixed
with charcoal and sulfur is highly unstable and is not to be used. |
|
|
It is difficult to locate ignition
temperatures for pyrotechinic compounds but you can see by looking at those
above that there is a huge difference in the ignition temperature.
Generally, the lower the ignition temperature, the easier it will be to
ignite. Our igniter wire must not only reach the ignition temperature
but well above it so that it ignites the pyrogen quickly and surely.
Note that standard black powder with sulfur has the lowest ignition
temperature of those listed above. This is one reason it makes a good
pyrogen.
Another factor is how long it takes for
the igniter wire to get up to an ignition temperature. If there were
no heat transfer away from the igniter, you could apply a very low current
and in time it the temperature would increase to the ignition temperature.
However, anytime there are two materials at different temperatures, there
will be heat transfer. The bigger the difference in the temperatures,
the faster the heat will transfer. So we want the igniter to come to
temperature quickly, ignite the pyrogen, then melt the wire so that the
circuit is broken and no more current can flow to run down the battery.
What is fast enough? Ten seconds is too slow. One second is
slower than we would like. A tenth of a second or faster is good. How high should the
temperature be? Probably twice the ignition temperature.
Actually, the melting temperature of the igniter wire is what you will get
because it will keep getting hotter until it burns through at the melting
temperature. The only other possibility is that if the current is too
low, the heat will transfer out through the pyrogen to the pyrogen surface
and to the air and an equilibrium temperature will be reached where it will
get no hotter. If this temperature is below the pyrogen ignition
temperature, the igniter will never fire.
Example Igniters
So lets look at three examples.
(note "*" is used for multiplication per normal alegbra rather than x)
We will initially plan to use a 9V
alkaline battery and see if it would fire the igniter. We don't know
what the internal resistance is for sure but it is probably between 2.8 and
4.5 ohms so we will use 4.5 ohms.
#1 1" of 40 ga Nichrome wire
Looking up the values in the Misc. Tables
gages we find:
wire dia = 0.0031" = 3.1*103 in
ρ
= 39.4 μohm-in = 39.4*10-6
ohm-in
We can calculate:
A =
πd2/4 = 3.14*.00312/4
= 7.55 x 10-6
R = ρL/A ρ has a 10-6
in it and so does the area so if we drop both of those,
and since L = 1, we can just divide the ρ
number by the A number. Thus:
39.4 / 7.55 = 5.22 Ω
This is the same as
ρL/A = (39.4 * 10-6
* 1) / (7.55 * 10-6) = 5.22 Ω
Add in the battery internal resistance:
5.22 + 4.5 = 9.72 Ω
The current will be: I=E/R, I = 9/9.72 =
0.926A
The current through the internal resistance and load resistance (igniter
wire) is the same but the I2R heating of the igniter wire has to
be calculated using only the resistance of the wire.
So the power dissipated will be (.926)2 * 5.22 = 3.04 W.
Can an alkaline 9v battery deliver 0.926A? Yes.
#2 1" of 40 ga 304V Stainless
Steel wire
Looking up the values in the Misc. Tables
gages we find:
wire dia = 0.0031" = 3.1*103 inches
ρ
= 28.3 μohm-in = 28.3*10-6
ohm-in
We can calculate:
A = same as #1 = 7.55 x 10-6
R = 28.3 / 7.55 = 3.75 Ω
Add in the battery internal resistance:
3.75 + 4.5 = 8.25Ω
The current will be: I=E/R, I = 9/8.25 =
1.09A
The power dissipated will be (1.09)2 * 3.75 = 4.45 W.
Again, no problem delivering the current.
#3 1" of 39 ga copper wire
Looking up the values in the Misc. Tables
gages we find:
wire dia = 0.0035" = 3.5*103 inches
ρ
= .681 μohm-in = .681*10-6
ohm-in
We can calculate:
A =
πd2/4 = 3.14*.00352/4
= 9.62 x 10-6
R = .681 / 9.62 = .071 Ω
Add in the battery internal resistance:
.071 + 4.5 = 4.57Ω
The current will be: I=E/R, I = 9/4.57 =
1.97A
The power dissipated will be: (1.97)2 * .0708 = 0.275 W.
This is a very low power and will not even begin to heat up this igniter
wire. Instead, all we are doing is heating up the battery. A 12V car battery or garden tractor battery
will be required to fire this igniter. These have very low internal
resistance and so can fire an igniter made with any kind of small diameter
wire.
So why will a car battery fire this igniter. Let's calculate the
current. The difference is the internal resistance of the battery.
Typical car batteries can run in the range of 0.1 to 0.4 ohms internal
resistance. Lets use the worst case and call it 0.4 ohms
The total resistance would then be 0.4 + .071 = 0.47Ω
The current will be: I=E/R, I = 12/0.47 = 25.5A
The power dissipated will be: (25.5)2 * .0708 = 46 W.
Wow! Obviously, the igniter wire will burn through almost instantly
but will still deliver a healthy amount of heat.
From these calculations, you can get a good ball park idea of what will
work, what won't work and why.
Electric Matches and Igniters
In rocketry, the term "electric match"
is used for an igniter used to ignite an ejection charge using an altimeter
or electric timer in a rocket. You obviously can't launch a car
battery (or wouldn't want to) and so you need to use a small battery and 9V
alkaline batteries are very common. Since these delivery a lot less
current, the electric match is made to ignite with a lot lower current.
"Igniter" is the term that is used for igniters used to ignite rocket
motors. They typically require more current but also deliver more heat
and sometimes for a longer time. Motors take a lot more heat energy to
ignite than 4F black powder used for ejection charges.
| |
|
Side note:,
you may wonder why 4F is used for ejection charges. 4F can be
harder to find because it is used in black powder pistols where 3F
or larger grain sizes are used in black powder rifles which are much
more common. The smaller the number of "F"s, the larger the
grain size. The smaller the grain size, the easier it is to
ignite. You want the easiest and so most sure to ignite black
powder because it is so important that the ejection charge goes off.
If it doesn't, it usually means a "lawn dart," a rocket that comes
down nose first at extreme speed (very aerodynamic) and destroys
itself on impact with the ground, burying itself at least partially
if the ground is at all soft. You can use 3F but there is just
less room for error and so a lower confidence level. |
|
|
Electric matches are common in the pyrotech
(fireworks) business and that is what they call all their igniters. I
am pretty sure they use car batteries for ignition so their igniters are
probably more like our motor igniters. Bottom line is that the
differentiation between an "electric match" and an "igniter" is more of a
recent adoption and not an explicit difference. An "igniter" could
refer to both types, an "electric match" will normally refer to an igniter
used for igniting the recovery system charge though it could also be used in
a smaller motor. If you buy commercial igniters, just be sure to read
what they are for, and how much current is required to fire it.
| |
|
CAUTION: DO NOT USE LOW CURRENT IGNITERS FOR
MOTOR IGNITION WITH A STANDARD LAUNCH SYSTEM. Igniters
intended for use for ejection charges and low current can be fired
by the continuity circuit in a standard launch system. Most
launch systems use a light bulb in series with the igniter to show
that there is continuity through the igniter. A normal motor
igniter takes a fairly high current to fire so the small current for
continuity indication will not fire them. However, igniters
(electric matches) intended for ejection charges are designed to
fire with a very low current. If these are used in a motor,
they can ignite when hooking up the alligator clips and launch the
rocket with your hands under the exhaust resulting in severe burns
or much worse if the motor happens to CATO. For safety
purposes, the launch system should not be connected to the battery
at all when connecting the igniter leads and until all people are at
a safe distance from the rocket. |
|
|
See the
Homemade Wire-wound Igniters
page for construction details on these type igniters.
Home ||
High Power Rocketry ||
Experimental Rocketry
|
